Splines to Gcode from dxf file

Hi,

The G5 splines were a bit of a push-and-run rather a long time ago. I have a feeling that they were a masters project and then the author moved on.
Ok. Nice to know.

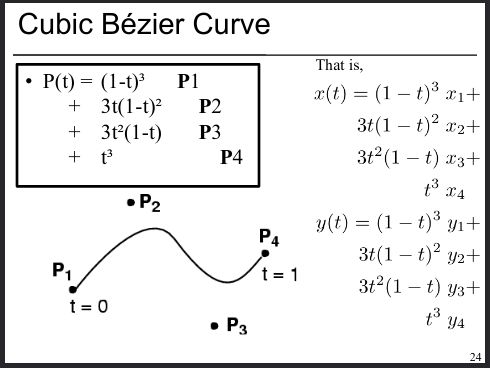
linuxcnc spline algo found in this document page 24

 

It's a cubic bezier curve.... Not even a spline.
 

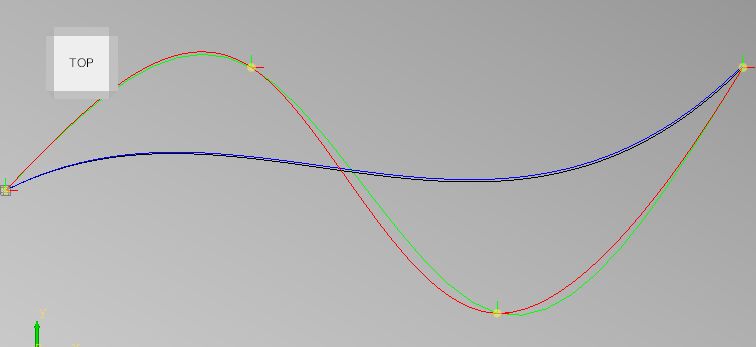
The testcase :

Result :

I gave them a offset of 1mm in y to show them both.
 
 

But even the cubic splines (red+green) algo's can be improved by making it a "true spline"

The so called "true spline" solution i found ~2~3 years ago while playing with the splines.

The defenition of a "true spline" is a spline wich is identical in both 2 states. The first stage is a forward sweep, the second
stage is a backward sweep. The differential result from time 0-1 is a "true spline".

This type of spline is never used on the stock marked for sure !




 

Thanks for being busy on that. Yes it is the Bezier form of a spline. Spline means its a piesewise polynomial that is smooth; thats all. The first argument is the start point, current position P0. The endpt P2 for quadratic feed and P3 for cubic feed. The arguments inbetween are not waypoint/nodes/knots; it is one controlpoint for quadratic and 2 for cubic spline. Task is to figure out the position of the control points to match 'black to 'green curve; fix the boundary constraints.
Then potentially add some code to linuxcnc to scale contributions t2 and t3 accordingly, or pass G5 I,J,P,Q arguments through an additional calculation step.

Task is to figure out the position of the control points to match 'black to 'green curve;
Ahh.
I found this convert example
But i am stuck at (16)  b=2 c=2. I don't get where they get the b and c values from.
And where they fill in the cubic spline control points.

It looks like the lcnc master, file : gcodemodule.cc has not the spline code inside anymore.
So it's what any suggested, the code should be somewhere else.
 

I gave it a further try to resolve the inconsistencies observed. I did commit addition files to
github.com/Matttab/spline-examples


including a translation to GNU octave of SPLINE_FEED for 4 input arguments generating a 2nd order polynomial and for SPLINE_FEED using 6 input arguments generating the most commonly used 3rd order polynomial.

I agree with previous posts - it is a Bezier type of spline going from startpoint at P0=(x0,y0) to the endpoint P3=(x3,y3). The interior points P1 and P2 are not way points, but so-called control points, defining the actual shape of the curve.
File Attachment:

An example fit of one cubic spline segment to 4 way points and the subsequent high-resolution interpolation is given on github.

The required control points can be calculated from the derivatives of your spline at the start and end of each segment. For any G5 move, the first Point x1,y1 will define the initial slope. This should match the slope of any precedent straight line G1 move, or any precedent G5 slope at end point. The second Point x2,y2 will define the end slope. This should match the slope of any subsequent straight line G1 move, or any subsequent G5 slope at start point.

For any repeated and smoothly attached spline segment G5(P,Q), the initial slope will already be defined by the previous G5 P and Q arguments. This is why I,J are only required for the first segment in a multi-segment spline.

As far as I understand it, I,J, P, and Q are actually absolute coordinates. However, I,J relative to x0,y0 define the initial slope and P,Q, relative to x3,y3 define the end slope - that's the relative interpretation.

The spline_constructor() actually works as well. Implemented is some efficient algorithm to reconstruct a spline with N segments through the N-Points given into to the spline_constructor as input argument. However, the boundary conditions are only correct, if the tangent at the start and end are added to the input as first and last point. The spline_constructor() will always connect a two-point vector input by a straight line as long as no further interior points are given. Also, coefficients are calculated in the canonical basis (1,t,t^2,t^3) and not in the Berstein basis.

For a sequence of type: straight line, spline, straight line, simply add the first and last point of the straight line segments to the spline_constructor() input to join the spline smoothly to the straight line ends. If the spline_constructor() is used only for graphics output, I guess that's fine. Evt. it does not look the same as in the dxf or in the actually milled part.

I have tested autodesk fusion 360. It provides a spline definition by use of control points. The definition should agree with the Feed command from linuxCNC. However, no benefit there, the output will not contain any G5 but only G1 moves.